مقایسه با بازگشت اضافی

مرتب سازی به ترتیب هزینه اولیه

محاسبه نرخ بازگشت سرمایه

نرخ بازگشت < حداقل نرخ جذاب :حذف از مقایسه

مقایسه دو به دو با روش تحلیل بازگشت اضافی

بازگشت اضافی تفاضل درآمد و هزینه > نرخ جذاب : پروژه گران تر ، اقتصادی تر

اونی که کمتر از نرخ جذاب است ،حذف میشود .

\(ROR_\Delta > MARR\)

مثال 1

مثال-5-8- سه طرح A و B و C با مشخصات زیر در اختیار است.عمر مفید هر طرح 20 سال و ارزش اسقاطی آنها صفر فرض می شود .اگر حداقل نرخ جذب کننده 6% فرض شود کدام یک از این سه طرح ناسازگار، اقتصادی ترین است؟

\(-2000\)

\(+410(\frac{P}{A},ROR,20)=0\)

\((\frac{P}{A},ROR,20)=\frac{2000}{410}=487\)

\(ROR = 20%\)

\(MARR=6%\)

\(\frac{\Delta}{12-15}=\frac{7.14-6.46}{7.47-6.26}\)

\(\Delta=-2.18\)

\(ROR=15-2.18=12.82\)

\(ROR=-(4000-2000)\)

\(+(639-410)(\frac{P}{A},ROR,20)=0\)

\((\frac{P}{A},ROR,20)=\frac{4000-2000}{639-410}=8.73\)

\(\frac{\Delta}{10-9}=\frac{8.73-8.514}{9.129-8-514}\)

\(\Delta=0.35\)

\(ROR=9.65%\)

\(ROR=-(5000-4000)\)

\(+(700-639)(\frac{P}{A},ROR,20)=0\)

\((\frac{P}{A},ROR,20)=\frac{5000-4000}{700-639}=16.39\)

\(\frac{\Delta}{2-1.75}=\frac{16.39-16.753}{16.35-16.753}=0.22\)

\(ROR=1.97<6%\) گزینه B اقتصادی تر است

مثال 2

مثال-4-8-خرید یکی از دو ماشین X و Y مورد نظر است. با استفاده از روش ترسیمی تجزیه و تحلیل سرمایه گذاری اضافی ، اقتصادی ترین ماشین را انتخاب کنید . حداقل نرخ جذب کننده 10% فرض شده است.

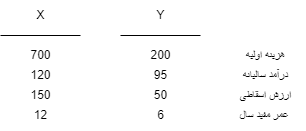
\(NUV_X = -200(\frac{A}{P},ROR,6)\)

\(+95\)

\(+50(\frac{A}{F},ROR,6)=0\)

\(NUV_Y = -700(\frac{A}{P},ROR,12)\)

\(+120\)

\(+150(\frac{A}{F},ROR,12)=0\)

ROR	\((\frac{A}{P},ROR,6)\)	\((\frac{A}{F},ROR,6)\)	NUV
15	0.1845	0.0345	-3.9
10	0.1468	0.468	24.26
7	0.1259	0.0559	40.25

ROR	\((\frac{A}{P},ROR,12)\)	\((\frac{A}{F},ROR,12)\)	NUV
7	0.2098	0.1398	60.03
10	0.2296	0.1296	55.56
20	0.3007	0.1007	39.89
40	0.4613	0.613	5.8
50	0.5758	0.0481	-17.75

\(NUV = -700(\frac{A}{P},ROR,12)\)

\(+200(\frac{A}{P},ROR,6)\)

\(+150(\frac{A}{F},ROR,12)\)

\(-50(\frac{A}{F},ROR,6)=\)

گزینه X اقتصادی تر است.

مثال 3

مثال-8-8 سه پروژه A و B و C را با استفاده از روش نرخ بازگشت سرمایه باهم مقایسه نمایید.عمرمفید پروژه ها 20سال و حداقل نرخ جذب کننده 6% فرض می شود.اقتصادی ترین پروژه را تعیین کنید.

\(ROR=2000(\frac{A}{P},ROR,20)=410\)

\((\frac{A}{P},ROR,20)=\frac{410}{2000}=0.205\)

\(ROR=4000(\frac{A}{P},ROR,20)=639\)

\((\frac{A}{P},ROR,20)=\frac{639}{4000}=0.16\)

\(ROR=5000(\frac{A}{P},ROR,20)=700\)

\((\frac{A}{P},ROR,20)=\frac{700}{5000}=0.14\)

\(A,B=(\frac{A}{P},ROR,20)=\frac{639-410}{4000-2000}=0.114\)

\(ROR=9-10%>MARR=B\)

\(B,C=(\frac{A}{P},ROR,20)=\frac{700-639}{5000-4000}=0.061\)

\(ROR=2%<MARR=B\)

مثال 4

مثال-10-8اطلاعات زیر در مورد پنج پروژه ناسازگار در اختیار است.نرخ بازگشت سرمایه هر پروژه قبلا محاسبه شده است. با استفاده از روش نرخ بازگشت سرمایه اقتصادی ترین پروژه را انتخاب کنید.عمر هر پروژه 20سال و MARR=6% است.

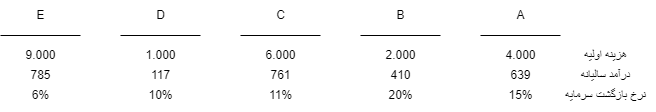
\(MARR=6%\)

مثال 5

مثال11-8-شرکتی خرید یک ماشین تراش را بررسی می کند.شرکت قادر است ماشین تراش جدیدی را به قیمت210.000 واحد پولی و یایک ماشین تراش پنج سال کارکرده را به قیمت 150.000 واحد پولی خریداری نماید.هزینه سالیانه ماشین جدید 70.000 در سال در حالیکه برای ماشین کارکرده 82.000 واحد پولی در سال می باشد.عمر مفید 25 سال برای هر دو ماشین با ارزش اسقاطی معادل 5% هزینه اولیه فرض می شود.اگر MARR=15%باشد،خرید کدام ماشین تراش اقتصادی تر است؟

مثال 6

مثال 12-8-یک شرکت تولیدی لباس بچه گانه،خرید یک ماشین خیاطی را با در اختیار داشتن اطلاعات زیر در مورد ماشین خیاطی اتوماتیک و نیمه اتوماتیک بررسی میکند.اگر حداقل نرخ جذب کننده 15% باشد کدام ماشین خیاطی را باید خریداری نماید؟

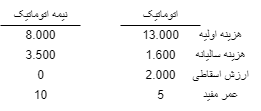
\(ROR_A =NPV=-13-1.6(\frac{P}{A},ROR,5)\)

\(+2(\frac{P}{F},ROR,5)=0\)

\(ROR_S =NPV=-8-3.5(\frac{P}{A},ROR,10)=0\)

\(-13-1.6(\frac{P}{A},ROR,5)+2(\frac{P}{F},ROR,5)\)

\(+8+3.5(\frac{P}{A},ROR,10)=0\)

\(ROR>MARR\)

|ROR|\((\frac{P}{A},ROR,5)\)|\((\frac{P}{F},ROR,5)\)|NPV| این روش جواب نمیدهد.

مثال 7

مثال 13-8-نرخ بازگشت سرمایه را در پروژه زیر با عمر مفید 10 سال محاسبه کنید.متذکر می شود که در سال چهارم شرکت مربوطه مجبور به سرمایه گذاری در خط تولید خود می باشد.

سال	فرایند مالی	سال	فرایند مالی
۱	۲۰۰	۶	۵۰۰
۲	۱۰۰	۷	۴۰۰
۳	۵۰	۸	۳۰۰
۴	۱۸۰۰-	۹	۲۰۰
۵	۶۰۰	۱۰	۱۰۰

\(NPV=200(\frac{P}{F},ROR,1)\)

\(+100(\frac{P}{F},ROR,2)\)

\(+50(\frac{P}{F},ROR,3)\)

\(-1800(\frac{P}{F},ROR,4)\)

\(+600(\frac{P}{F},ROR,5)\)

\(+500(\frac{P}{F},ROR,6)\)

\(+400(\frac{P}{F},ROR,7)\)

\(+300(\frac{P}{F},ROR,8)\)

\(+200(\frac{P}{F},ROR,9)\)

\(+100(\frac{P}{F},ROR,10)=580.2452\)