دوره نامتناهی
\(A = p \frac {i ( 1 + i )^n}{( 1 + i )^n -1}\)
\(A = \lim_{n\to\infty} P\frac {i(1+i)^n}{(1+i)^n -1}=P.i\)
\(P=\frac{A}{i}\)
مثال 1
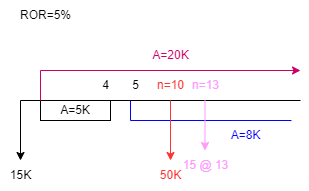
مثال 5-6- یک سد کوچک دارای هزینه اولیه 150000 واحد پولی و همچنین سرمایه گذاری جدیدی به مبلغ 50000 واحد پولی در سال دهم خواهد داشت . هزینه سالیانه در چهار سال اول 5000 واحد پولی و از سال پنجم به بعد 8000 واحد پولی خواهد بود . این سیستم هر 13 سال یکبار نیاز به یک تعمیرات کلی دارد که مبلغ آن 15000 واحد پولی پیش بینی می شود . اگر برای این پروژه 20000 واحد پولی باشد ، آیا ایجاد این سیستم آبیاری اقتصادی است ؟
پاسخ مثال 5-6
\(NUV=-150 \times 0.5\)
\(-50(\frac{P}{F},5,10)\times 0.5\)
\(-5(\frac{P}{A},5,4)\times 0.05\)
\(+20\)
\(+8(\frac{P}{A},5,4)\times 0.05\)
\(-8\)
\(-15(\frac{A}{F},5,13)\)
مثال 2
مثال 6-6- یک متخصص آب برای تامین آب یک شهر دو سیستم را ارائه می کند . اول ایجاد یک سد ، با هزینه اولیه 8 میلیون و هزینه سالیانه 25000 واحد پولی . ( این سد دارایی عمر نامحدود خواهد بود ) دوم ، حفر چاههای عمیق و انتقال آب به شهر به وسیله لوله . این متخصص پیش بینی می کند که 10 چاه برای تامین آب شهر مورد نیاز باشد هزینه اولیه هر چاه 45000 واحد پولی خواهد بود که شامل لوله کشی نیز میشود . عمر هر چاه 5 سال در نظر گرفته شده و هزینه سالیانه هر چاه 5000 واحد پولی خواهد بود . اگر حداقل نرخ جذب کننده را 5 % در نظر بگیریم ، کدام پروژه را انتخاب می کنید ؟
پاسخ مثال 6-6
1: سد
هزینه اولیه 8M=8000K
هزینه سالیانه 25K
عمر نامحدود
نرخ جذاب 5%
\(NUC_1=8000\times 0.05 + 25 =425K/yr\)

2 : چاه عمیق + لوله
تعداد چاه 10
هزینه اولیه هر چاه 45K
عمر هر چاه 5 سال
هزینه سالیانه 5K
\(NUC_2=10[45(\frac{A}{P},5,5)+5]=153.95K\)
\((\frac{A}{P},5,5)=0.2310\)

دومی اقتصادی تر است .
مثال 3
مثال 5-7- شخصی 10000 واحد پولی را اکنون ، 30000 واحد پولی سه سال دیگر و 6000 واحد پولی را از سال چهارم تا هشتم در بانکی پس انداز می کند . درآمد یکنواخت سالیانه حاصل از این سرمایه گذاری از سال دوازدهم تا مدت نا محدود چقدر خواهد بود ، اگر نرخ بهره سالیانه بانک 8% در سال باشد .
پاسخ مثال 5-7
اکنون 10K
سه سال دیگر 30K
سال 4 تا 8 6K
نرخ بهره 8 %
درآمد یکنواخت از سال 12 به بعد (نامحدود ) =؟
\(F=10(\frac{F}{P},8,11)\)
\(+30(\frac{F}{P},8,8)\)
\(+6(\frac{F}{A},8,5)(\frac{F}{P},8,3)=123.2K\)
\((\frac{F}{P},8,11)=2.332\)
\((\frac{F}{P},8,8)=1.851\)
\((\frac{F}{A},8,5)=5.867\)
\((\frac{F}{P},8,3)=1.26\)
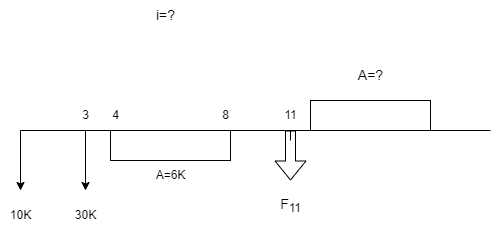
\(P_n => A_{\infty}=123.2 \times 0.08 = 9.856K\)
مثال 4
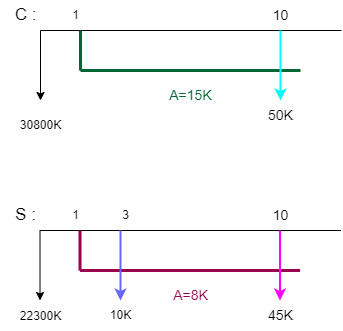
مثال 8-7- شهرداری اهواز بررسی اقتصادی دو پل بتنی و فلزی را بر روی رودخانه کارون آغاز نموده و انتخاب یکی از دو پل ضروری است . هزینه اولیه پل بتنی 30/8 میلیون واحد پولی ، هزینه تعمیرات سالیانه 15000 واحد پولی و هزینه بازرسی و کنترل 50000 واحد پولی برای هر ده سال یکبار است . پل فلزی دارای هزینه اولیه 22/3 میلیون هزینه تعمیرات سالیانه 8000 واحد پولی ، هزینه رنگرزی هر سه سال یکبار 10000 واحد پولی و هزینه بازرسی و کنترل هر ده سال یکبار 45000 واحد پولی است . عمر پلها نامحدود و حداقل نرخ جذب کننده 6 % فرض می شود . با استفاده از روش EUAC اقتصادی ترین طرح را تعیین نمائید .
پاسخ مثال 8-7
| C | S | |
|---|---|---|
| 30.8M | 22.3M | هزینه اولیه |
| 15K | 8K | تعمیرات سالیانه |
| 50K@10 | 45K@10 | هزینه بازرسی و کنترل |
| 10K@3 | رنگرزی | |
| بی نهایت | بی نهایت | عمر |
\(MARR=6%\)
\(C: 30800 \times 0.06\)
\(+15\)
\(+50(\frac{A}{F},6,10)=1866.79K\)
\(S: 22300 \times 0.06\)
\(+8\)
\(+45(\frac{A}{F},6,10)\)
\(+10(\frac{A}{F},6,3)=1352.55K\)