سری هندسی

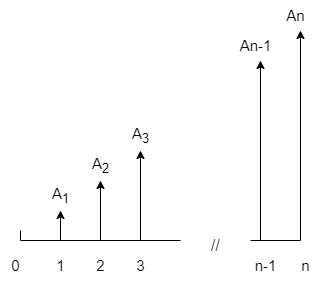
هر تراکنش نسبت به دوره قبل به اندازه j درصد افزایش یا کاهش دارد.

\(A_t = A_{t-1}(1+j); t=2,3,...,n\)

\(A_t =A_1(1+j)^{t-1}; t=1,2,...,n\)

ارزش فعلی

\(P = A_1 \frac {(1+j)^{t-1}}{(1+j)^t}=\begin{cases}\frac{A_1}{i-j}(\frac{1+i}{1+j})^n & i\neq j\\ \frac{nA_1}{1+i}&i=j\end{cases}\)

\(P= \sum A_1 \frac {1-(F/P,j,n)(P/F,i,n)}{i-j} \ j\geq0 , i\neq j\)

ارزش آتی

\(F= \begin{cases} \frac{A_1}{i-j}((1+i)^n-(1+j)^n) & i\neq j \\ nA_1(1+j)^{n-1} & i=j \end{cases}\)

\(F= A_1 \frac{1-(F/P,j,n)(P/F,i,n)}{i-j}(F/P,i,n) j\geq 0 , i\neq j\)

مثال 1

مثال 6-4-شرکت " گلسرخ " پیش بینی کرده که هزینه های نیروی انسانی آن شرکت 8% در سال افزایش دارند . این شرکت علاقمند است بداند که چه مقدار سرمایه را امروز باید در بانکی پس انداز کند تا هزینه های نیروی انسانی 5 سال آینده تامین گردد ، نرخ بانک 10 % در سال است و هزینه های نیروی انسانی سال آینده شرکت 50000 واحد پولی است.

مثال 2

مثال 7-4- درآمد حاصل از فروش دارویی مخصوص در شرکت داروسازی " گل دارو " هر ساله 10 % افزایش دارد . شرکت دارای حداقل نرخ جذب کننده 8 % در سال می باشد و در آمد سال آینده شرکت 50000 واحد پولی است . ارزش آینده درآمد ها در پایان سال دهم چقدر خواهد بود ؟ داده های مسئله عبارتند از :

نرخ اسمی و موثر

\((1+i_e)=(1+\frac{r}{t})^t\)

مثال 1

مثال 2-5- شرکت " گل ابزار " قصد خرید یک ماشین صنعتی را به قیمت 45000 واحد پولی دارد و بانکی حاضر است این مبلغ را به شرکت قرض بدهد . نرخ بانک 12 % در سال می باشد . شرکت باید مبلغ فوق را در مدت سه سال به اقساط ماهیانه پرداخت نماید . قسط ماهیانه شرکت چقدر خواهد بود .

مثال 2

مثال 4-5- شخصی علاقمند است مبلغی را به عنوان سپرده ثابت در بانک پس انداز کند . نرخ بانک 8 % در سال و بهره بصورت روزانه پرداخت می شود . نرخ موثر سالیانه و نرخ موثر شش ماهه را تعیین کنید .

مرکب پیوسته

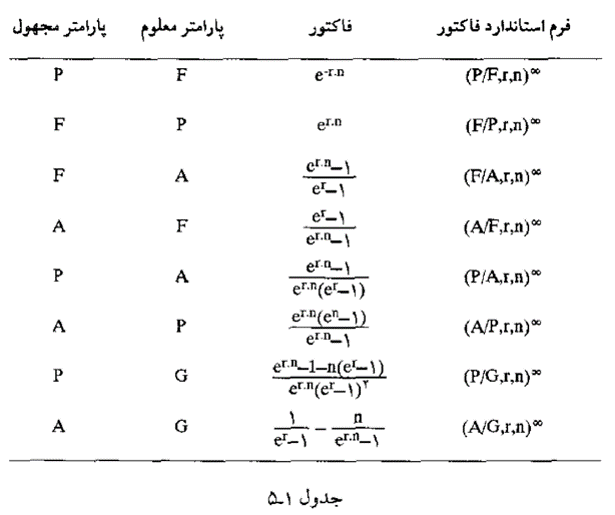
\(F=P (\lim_{t\to\infty}(1+\frac{r}{n})^{tn})=Pe^{rn}\)

مثال 1

مثال 5-5- اگر 200000 واحد پولی با نرخ 12% در سال بطور مرکب پیوسته سرمایه گذاری شود ، پس از 5 سال اصل و فرع چقدر خواهد بود ؟