شیب یکنواخت
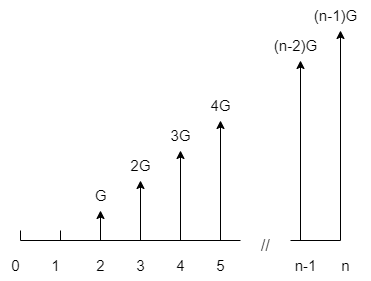
شکل جریان به شکل مثلث است . G نشان دهندۀ این است که در هر دوره ، جریان مالی چقدر افزایش یا کاهش یافته است . G دارای یک راس و یک دستۀ پرچم است نکته ای که وجود دارد این است که راس باید سمت چپ باشد .
مثلث
1.مشخص کردن مقدار G (یک دندانه را در نظر میگیریم و با دندانۀ کناری آن مقایسه می کنیم و مقدار G را به دست می آوریم . )
2.راس
3.دسته پرچم
مثال 1
4-1-شرکت " گلپا " علاقمند است ارزش فعلی فرآیند مالی زیر را محاسبه کند ، حداقل نرخ جذب کننده 5% در دورۀ در نظر گرفته شده است .
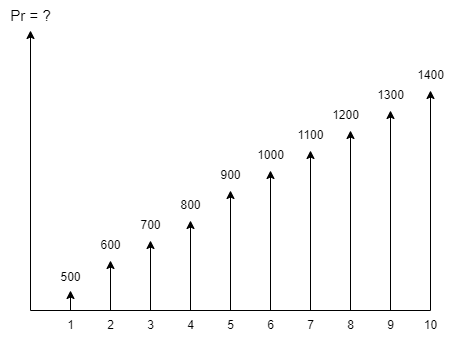
پاسخ مثال 1
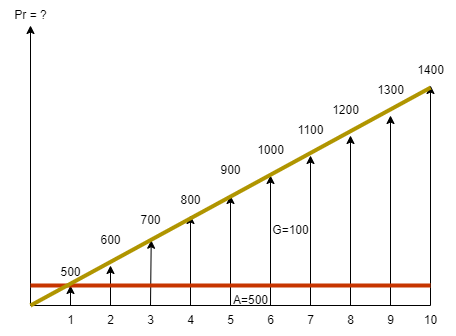
\(P=500(\frac{P}{A},5,10)\)
\(+100(\frac{P}{G},5,10)=\) \(7026\)
\(P(\frac{P}{A},5,10)=7.722\)
\(P(\frac{P}{G},5,10)=31.652\)
مثال 2
2-4-مقدار در آمد سالیانه یکنواخت (A) را در مثال 1-4 محاسبه کنید .
روش اول :
\(A=500\)
\(+100(\frac{A}{G},5,10)\)
\(=910\)
\((\frac{A}{G},5,10)=4.099\)
روش دوم :
\(A=7026(\frac{A}{P},5,10)\)
\(=910\)
\((\frac{A}{P},5,10)=0.1295\)
مثال 3
4-3-میزان هزینه های سالیانه تعمیرات و نگهداری ماشین آلات در شرکت " گل آرا " طبق فرآیند مالی زیر برآورده شده است . حداقل نرخ جذب کننده 5% در سال فرض شده و اعداد بر حسب 1000 هستند . ارزش فعلی هزینه ها را محاسبه نمائید .
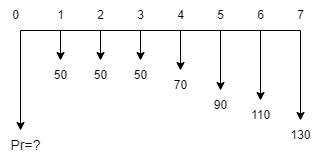
پاسخ مثال 3

\(P=50(\frac{P}{A},5,7)\)
\(+20(\frac{P}{G},5,5)(\frac{P}{F},5,2)=439\)
\((\frac{P}{A},5,7)=5.786\)
\((\frac{P}{G},5,5)=8.237\)
\((\frac{P}{F},5,2)=0.9070\)
مثال 4
4-4-ارزش فعلی فرآیند مالی زیر را با نرخ 7% در سال محاسبه نمائید .
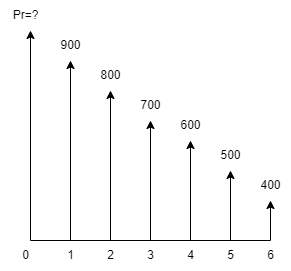
پاسخ مثال 4
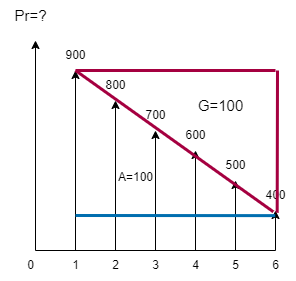
\(P=900(\frac{P}{A},7,6)\)
\(-100(\frac{P}{G})=3192\)
\(P(\frac{P}{A},7,6)=4.767\)
\(P(\frac{P}{G},7,6)=10.978\)
مثال 5
4-5-طرح تولید میز تحریر خاصی به شرکت " گل ابزار " پیشنهاد شده است . فرآیند مالی محصول عبارت از سرمایه گذاری های متعدد در 5 دوره و سپس فروش محصول و کسب در آمد در 7 دورۀ بعد است ، شکل فرآیند مالی بصورت زیر است . نرخ جذب کننده برای شرکت 7% در دوره می باشد . آیا با استفاده از روش ارزش فعلی می توان گفت این طرح اقتصادی است ؟
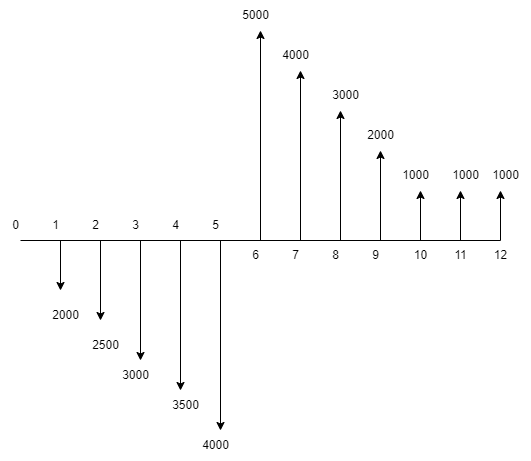
پاسخ مثال 5
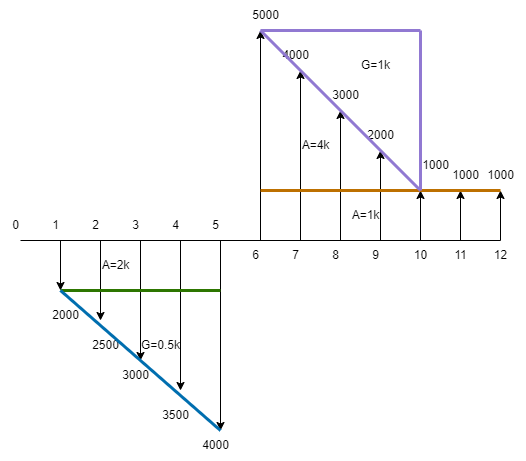
\(P=-2k(\frac{P}{A},7,5)\)
\(-0.5k(\frac{P}{G},7,5)\)
\(+[4k(\frac{P}{A},7,5)\)
\(-1k(\frac{P}{G},7,5)\)
\(+1k(\frac{P}{A},7,5)]\times (\frac{P}{F},7,5)=\)
\((\frac{P}{A},7,5)=4.100\)
\((\frac{P}{G},7,5)=7.641\)
\((\frac{P}{F},7,5)=0.7130\)