هم ارزی

\(ارزش= f(زمان,پول)\)

ارزش پول در طول زمان تغییر می کند . تورم را نمیتوان تعیین کرد ولی نرخ بهره تعیین می شود .

مثال

با نرخ ۶٪ ، ۱۰۰تومان الان = ۱۰۶ تومان سال بعد

P=F, P≠F

نرخ بازگشت سرمایه Rate of return (ROR)

\(ROR =\frac{سرمایه اولیه - اصل و فرع }{سرمایه اولیه}\) \(=\frac{سود }{سرمایه}\)

تفاوت نرخ بازگشت با نرخ بهره

- حداقل نرخ جذاب Minimum Attractive Rate of return (MARR)

کمتر از آن جذاب (اقتصادی) نیست

بستگی به شخص

نرخ بهره یا free risk

cash flow نمودار جریان مالی

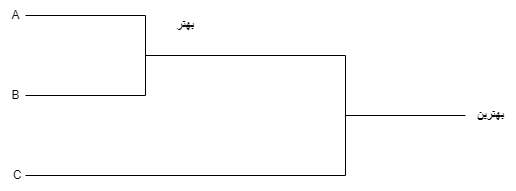
مثال 1

مثال ۳-۲- مبلغ ۲۰,۰۰۰ واحد پولی برای مدت ۵ سال با نرخ بهره سالیانه ۶٪ قرض گرفته شده است. مقدار اصل و فرع پول پس از ۵ سال بازپرداخت خواهد شد. شکل فریاد مالی را رسم کنید.

\(20k(1.06)=26.7k\)

مثال 2

مثال ۴-۲- اگر شخصی از امروز سال مبلغ ۱۰,۰۰۰ واحد پولی در بانکی با نرخ بهره ۷٪ در سال پس انداز نماید، پس از ۴ سال چه مقدار ب عنوان اصل و فرع در بانک خواهد داشت.

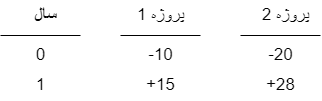
47.5 =10(\(1.07^4\))+10(\(1.07^3\))+10(\(1.07^2\))+10(1.07) موجودی

مثال 3

مثال ۵-۲- شرکت (گلناز) هفت سال پیش یک کمپرسور هوا را ۲۵,۰۰۰ واحد پولی خرید . درآمد سالیانه کمپرسور ۷,۵۰۰ واحد پولی بوده است. هزینه تعمیرات و نگهداری در سال اول ۱۰۰۰ واحد پولی، در سال دوم ۱،۲۵۰ واحد پولی و در سال سوم ۱،۵۰۰ واحد پولی بوده ، به همین ترتیب هر سال ۲۵۰ واحد پولی افزایش داشته است. شرکت قصد دارد کمپرسور را به مبلغ ۱,۵۰۰ واحد پولی (ارزش اسقاطی) در سال آینده بفروشد. شکل فرآیند مالی را رسم کنید.

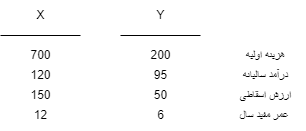
در اقتصاد مهندسی گذشته نداریم. راس مثلث حتما باید سمت چپ باشد. (اگر نبود باید یک مستطیل در نظر بگیریم و یک مثلث از آن کم کنیم.)